The Alpha 2 Rating System

For Sanctum: Revolutions, NIOGA has adopted a new rating system. This is based on the Alpha 2 rating system by Ian Schreiber, Genetic Anomalies/THQ, and With Authority!

Overview

Summary of Alpha 2

Automatic Rating Calculator

Rating Table

Questions

How do I become ranked?

What's new about Alpha 2?

What is the luck factor?

How can I win the most rating points?

Technical Details

Show me what the math looks like — but hold the math!

I can handle the math. Show me the math!

Example of Rating Calculation

Historical Notes

Converting Old Ratings to Alpha 2

How is Alpha 2 different from the old rating system?

Summary of Alpha 2

• A new ranked player starts at 1500 rating.
• Each game has a total purse of 32.0 points.
• The maximum rating difference is 600 points.
• The luck factor is 15%.
• Rating points are stored in floating-point, and are never rounded.  (They are truncated for display only.)
• A disconnected game now counts the same as if the disconnected player conceded.  The other player gets a win.

Automatic Rating Calculator. For your convenience, the Sanctum game challenge windows now include a built-in Rating Calculator.

• In the Challenge window, just click the “Ranked” button, and you'll instantly get a 1-line summary of the points you'll win or lose.

• When you receive a ranked challenge, the Ponder window also shows the same summary.

Rating Table. Calculate the rating difference as

(your rating - opponent's rating)

then look it up in the following table.

The Rating Calculator does this for you automatically whenever you compose or receive a ranked challenge.

Questions

How do I become ranked?
Your account becomes ranked when you buy enough cards for it. A new ranked account begins at a rating of 1500. Playing ranked games will raise or lower your rating.  Only ranked players may play ranked games.

What's new about Alpha 2?
NIOGA feels that the Alpha 2 rating system will be a more accurate measure of a player's skill. It is founded on the following premises:

1. Luck exists. Sometimes, no matter how good you are and how bad your opponent is, you'll lose anyway (as any Mage of Unmaking will tell you). It may not happen that often, but it does happen, so the rating system should take luck into account.
2. Games are zero-sum. When one player gains some points, the other player should lose the same number of points. Playing games should not create new points out of thin air, and they should not throw any points away.
   

What is the luck factor? The luck factor represents the idea that “luck exists”. Sanctum is a game of skill, but also a game of chance, and sometimes the two don't balance out.

1. Most wins are from skill. We assume that rating is mostly skill. If Anne is rated 2000, and Steve is rated 1400, we conclude that Anne is a better player. If Anne plays Steve many times, Anne should win most of those games.
2. Some wins are from luck. No matter how good you are, sometimes that Bolt of Somersaults will put the opponent's Horde on your doorstep. If Anne and Steve play often enough, Steve will score an upset win every now and then. The luck factor recognizes that Anne can't win every game. When she does lose, it probably isn't because Steve suddenly became a great player for one game. Instead, it's more likely that Steve benefited from good luck.

In a game of pure skill, at the maximum allowable rating difference, the higher player should win 100% of the time.  Then the reward for those wins should be 0 points. But even the best Sanctum player can't win 100% of the time, because of luck.

The luck factor gives a small amount of bonus points whenever the higher player wins a game. So the higher player wins a little, and the lower player loses a little more. Over many games, these small bonus points for the higher-rated player should add up and roughly cancel out the cost of losing the occasional game to bad luck. This can encourage high-rated players to keep playing games. (Conversely, whenever the lower player wins in a big upset, he has to pay a small “luck tax”, so he wins slightly fewer points than before.) 

How can I win the most rating points? A rating system measures skill. In the long run, the only way to permanently increase your rating is to get better at the game. Other than that, play people who are about as good as you are. This will get you an accurate rating in the fewest games. It should also give you the most fun and engaging gameplay.

Technical Details

Show me what the math looks like — but hold the math! The Alpha 2 rating formula is a slanted line.

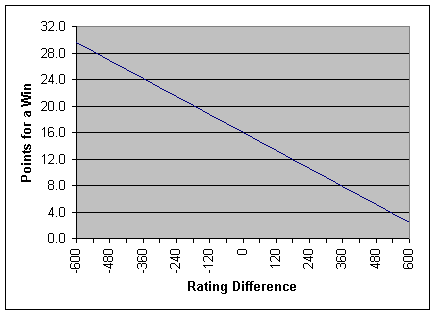
Figure 1. Alpha 2 rating system

• At 0 rating difference, both players are equally good, so they're equally likely to win. Out of fairness, Alpha 2 assigns equal risk to both players. Thus, they each risk half of the 32 point total purse for a game, or 16 points each. So the midpoint of the rating line, at a rating difference of 0, passes through 16.0 points.
• At the maximum rating difference of +600 points or higher, the winner would normally receive 0 points. Instead, the winner now receives a luck bonus of (luck factor) * (half purse), or 15% * 16.0 = 2.4 points. So the low end of the rating line passes through 2.4 points. The luck bonus is an incentive for the high-rated player to keep playing games.
• Put another way, if the high rated player loses a game at +600 difference, he will lose (32 * luck bonus) = 29.6 points. Then he has to win (29.6 / 2.4) = 12.3 out of (12.3 + 1), or a little better than 12 out of 13 games, just to break even. If he thinks he can do better than that, then he'd rather play than squat.

I can handle the math. Show me the math! Alpha 2 is ultimately just a straight line.  As you know, a straight line is defined by the equation y = mx + b.  Since we’re going to plot rating difference d horizontally, and points won w vertically, this becomes w = md + b.

You've already seen all of the constants that define Alpha 2.  Let's write them symbolically:

• Let M = 600 be the maximum rating difference.
• Let H = 16 be the half-purse between two equal opponents.
• Let L = 15% = 0.15 be the luck factor.
• Let S = (1 – L) = 0.85 be the skill factor.

At +M or higher rating difference, we assume that the lower player is completely outclassed, and could win only by luck. We assume that 85% of all games of Sanctum are decided by skill, and 15% are decided by luck. (This is NIOGA's best guess for now, and will be revised later as we acquire more data from real games.)

• Let d = winner's rating – loser's rating.  (Note that d could be negative!) Restrict d to lie in the range [–M, +M].
• Let w = rating points won.

Now, what's the slope of the rating line? We know that:

• At d = 0, we have w = H. Two even players risk H points each. Substituting into the line equation, we get H = m0 + b, or simply b = H.
• At d = +M, we have w = LH, by definition of luck factor L.

That's two points on the line. To calculate the slope m, simply calculate “change in y over change in x”, by definition of slope.

m = (LH – H) / (M – 0)

  = H (L – 1) / M

  = –HS/M

Plug this back into our line equation, and we get:

w = md + b

  = –(HS/M)d + H

  = H (1 – (S/M)d)

And that's it. The winner gains this many points, and the loser loses the same amount. Let's check this equation by verifying our two points.

• At d = 0, the (S/M)d term drops out, and we're left with w = H, as expected.
• At d = +M, d/M = 1.0, so the (S/M)d term reduces to S. Then the (1 – S) term is just L, by definition of S. Then we're left with w = HL = LH, as expected. (Conversely, at d = –M, we have w = (2 – L)H.)

Plugging Sanctum's constants into this equation, we get the final form:

            w = 16 (1 – 0.85 (d / 600))

Example of Rating Calculation. Anne at 2000 plays Jim at 1700. This gives d = +300.  Plugging in, we get

w = 16 (1 – 0.85 * (300 / 600)) = 16 * 0.575 = 9.2

• If Anne wins, she takes 9.2 points of Jim's points.
• If Jim wins, he takes (32 – 9.2) = 22.8 points from Anne.

Put another way, every rated game has a total purse of 32.0 points. Since Anne is expected to win about 5 out of 7 against Jim, she has to put up about 5/7 of the purse. So Anne puts up 22.8 points of the purse out of her rating, and Jim puts up 9.2 points out of his rating. Then the winner collects the whole purse. If Anne wins, she gets back the 22.8 she put in, and she collects +9.2 points profit, which was Jim's purse.

Historical Notes

Converting Old Ratings to Alpha 2. All ranked Sanctum accounts have been converted from the old rating to the new Alpha 2 rating system. The conversion uses the simple formula

New Rating = 1400 + 2 * Old Rating

Rank titles have been converted also, using the same formula, so they still mean the same thing. An Initiate is still an Initiate, and so on.

How is Alpha 2 different from the old rating system? The old rating system had 4 specific flaws.

1. Inflationary. The minimum rating was 1, and new players often reached it. Every time a player at rating 1 lost a ranked game, he could not lose any more points, but his opponent still gained the proper amount of points. This created new rating points out of thin air.
2. Deflationary. When a player disconnected in a ranked game, he got a loss, and lost his rating points, but his opponent did not get a win, and did not gain any points. This caused rating points to vanish from the player pool permanently. It also tended to discourage high-rated players from playing.
3. No luck bonus. It assumed that a player at +M rating difference would win 100% of the time. Since players realized they could not possibly sustain that rate, they tended to stop playing after they reached Enchanter status, out of fear of losing to a low opponent due to bad luck.
4. Rounding errors. It rounded rating gains to integers. Instead of a straight line, it was a staircase function, as shown below.

Alpha 2 fixes all of these problems.

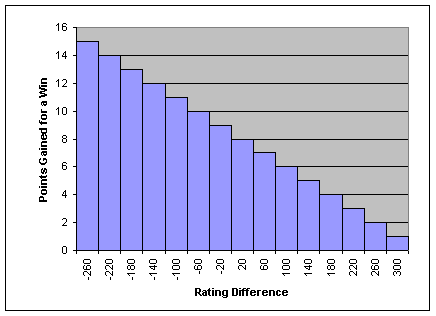
Figure 2. Old rating system

v2.20.00 Last updated 2009/03/21